新型有源滤波器的双向互补控制方案
摘 要:该文提出单周控制有源滤波器(UCI-APF)的双向互补控制方案。该方案通过双路控制方式来提高系统稳定性。与以往单周控制相比较,双向互补控制能有效扩大滤波器的稳定工作范围,消除进线电流直流分量与低频次谐波,从而解决了单周控制有源滤波器在实际场合应用的关键性问题。分析与实验结果验证了新方案的可行性。 关键词:有源滤波器;单周控制有源滤波器;双向互补控制 1 引言 谐波补偿与功率因数校正是近年来电力电子学的研究热点之一,有源滤波器(APF)则是谐波补偿的重要手段。APF[1]虽已有比较成熟的控制方法,但控制相当复杂,成本很高,仅能适合于大功率非线性负载的场合推广。因此在中、小功率非线性负载的场合需要研究APF的简单有效、低成本的控制方法。文[2]、[3]所提出的单周控制[2-7]有源滤波器(UCI-APF)是谐波补偿的一个新方向,可直接与设备连接消除谐波并调节功率因数接近于1,具有结构简便、无需产生电流基准以及采样通道少等诸多优点,非常适用于中、小功率的谐波抑制与功率因数校正。目前推出的是并联型有源电力滤波器。 现在UCI-APF采用的控制,由于固有的高频开关纹波和电路参数上的误差,主电路的电流难以避免有害的直流分量和低频次谐波,并且电路稳定工作范围有限[3],妨碍了其推广应用。针对这一情况,本文提出全新的双向互补控制原理。新方案的可行性通过了实验初步验证。
2 UCI-APF理论分析与直流分量问题 UCI-APF如图1所示,补偿电流由全桥逆变电路产生。
.jpg)
设有源滤波器开关频率为fs=1/T,全桥部分工作在2个状态:当0<t<DT时,Q1、Q4导通,Q2、Q3关断;当DT<t<T时,Q2、Q3导通,Q1、Q4关断。滤波器有效工作时,整个系统可等效为线性负载。根据理论分析,理想情况下系统进线电流与逆变器开关占空比之关系[2,3]为
.jpg)
式中 Re为补偿后的系统等效电阻性负载阻抗;Rs为电流采样电阻;D为开关占空比。 考虑到逆变器直流侧电压Vc在1个开关周期内基本不变,式(1)所表述的关系可通过单周控制的方式实现。设Ti=T/2,图1的控制部分满足单周控制方程[2,3]
.jpg)
因电路参数误差与温漂、时漂及老化等因素的影响,实际控制电路的积分时间常数无法做到十分精确。因此单周控制方程将修正为
.jpg)
k一般不能保证等于1,与式(2)对比,由式(4)计算得到的开关占空比将会偏大或偏小,其直接结果就是导致主电路上的进线电流存在直流分量。 此外,电流的高频开关纹波同样会构成对电路正常工作的影响[3]。根据单周控制原理分析,当电流单周积分到符合控制方程条件时刻,开关信号发生切换。因此,网侧电流峰值跟踪网侧电压的波形。图2即为电流高频纹波在包络线下方引起直流偏置和低频次谐波的示意图[3]。由于稳态时电流峰值与包络线相符,虚线所表示的低频平均值必然处于包络线下方。
.jpg)
电流直流分量的存在会引起继电保护装置误操作,还容易导致变压器饱和,其危害不可忽视。而积分时间常数的漂移将会导致系统工作不稳定。因此需要探索新的控制策略。
3 稳定性问题分析 对于UCI-APF电路,网侧进线电流小于基准波形时处于上升沿;当控制电路积分至满足控制方程时,电流与基准相等,电流开始下降,直至开关周期结束。因此电流波形如图2所示,进线电流处于参考波形下方。轻载情况下,系统容易在电流负半波出现不稳定。 根据开关变换器电流模式非线性控制的稳定性分析[4],电流上升、下降率与载波信号斜率之间必须满足一定关系。图3为电流与载波信号比较得到开关占空比的示意图。图中表示稳态进线电流;is为瞬时电流。系统稳定条件在于电流可趋向稳态,即在任一工作点开关占空比均可由瞬态值收敛至稳态值。
.jpg)
由图3可得相邻开关周期的占空比关系
.jpg)
式中 M1为电流上升率;M2为电流下降率;Mc为载波信号斜率;n表示第n个周期。 由式(5)可推出
.jpg)
当|(M2-Mc)/(M1 Mc)|<1时,占空比通过式(6)可经若干周期收敛至稳态值,各工作点的稳定性即由此判定[3,4]。 因此可推出系统稳定条件[3]
.jpg)
有源滤波器在电流处于工频周期正半波时-Vs< 0,必然满足稳定条件。但在负半波时则有可能不符稳定条件,因此最恶劣情况发生在轻载时的负半波峰值处。 解决稳定性问题的一个有效方法是设计双向对称的两路控制,单独工作时进线电流分别处于上、下参考波形之内,即系统在正、负半波时均自然满足稳定条件。若由两路控制切换工作,可使滤波器始终工作在稳定性较好的半波。
4 UCI-APF的双向互补策略 要让UCI-APF在实际场合推广应用,扩大电路稳定工作范围和消除直流分量十分必要。为此,双向互补策略采用双路控制,即通过切换使两路控制均在稳定性强的半波工作,同时部分消除直流分量,以提高系统性能。 由上文分析可知,通过式(2)的积分方式可以得到处于理想参考波形下方的电流波形。而对式(2)进行转换可得
.jpg)
式(8)即可作为双向互补策略需要的另一路控制方程。此时电流在每个开关周期内先下降后上升,积分电路需要计算的时间为(1-D)T。该路控制单独工作时电流处于理想参考波形上方,且在电流负半波系统自然满足稳定条件。 由上文稳定性分析,采用文[2]、[3]所介绍的原有单路控制时,电流处于参考波形下方,在电流正半波系统自然满足稳定条件,而在负半波稳定条件不能完全满足。双向互补控制的目标是在正半波采用原有控制策略,而在负半波采用电流处于参考波形上方的控制方式,从而使系统达到全局稳定。同时由于正、负半波对称控制,以及电流直流分量负反馈,直流分量问题得以改善。 理想情况下两路控制根据式(2)、(8)即可实现。但实际电路需要考虑积分时间常数和电流的开关纹波影响,必须对积分电路的基准信号进行校正。图4为经过补偿的双路控制模型,补偿后基准信号与积分器的关系满足理想的单周控制方程。
.jpg)
.jpg)
式中 ispk为电流峰值;is0为消除高频谐波后的低频电流;△iL为电流开关纹波峰的峰值。因积分时间常数误差和电流开关纹波的存在,双路控制方程将修正为
.jpg)
新策略的一个关键问题在于如何取得合适的补偿信号A1、A2,使修正后的控制方程与理想方程基本一致,从而实现网侧电流波形跟踪电压波的目标。 对于单路控制电路,用电流直流分量的负反馈可将直流分量调至零[5]。但考虑到电路稳定性的需要,双向互补策略采用双路切换控制。假设1路控制工作电流正半波,那么由2路控制的电流负半波无法反映1路控制的情况,反之亦然。此时仅由直流分量反馈无法同时对两路控制进行调节,过渡将出现交越失真。 解决交越失真问题,可由两路控制信号之差的负反馈实现。 因两路控制对称且共用一个积分电路,而积分器计算的分别为开关信号的高、低电平时间,积分时间常数误差和电流开关纹波影响将使两路控制信号出现对称性误差,即开关占空比分别偏大和偏小。这将直接影响主电路上进线电流,交越失真即由此引起。若以两路控制信号之差的积分作为负反馈,稳态时可将两路信号调至一致,实现平滑过渡。 考虑到残留直流分量问题,还需引入电流积分反馈。当积分时间常数大于工频周期时,此反馈信号即可体现进线电流直流分量,稳态情况下将直流分量调至零。 双向互补控制的具体做法就是将两路信号之<< p="">
提交
2025中欧绿色建筑工业化论坛9月北京启幕 全球智慧共推建筑产业“双碳”转型
喜讯!华强电子网荣获“2025年中国产业互联网创新企业”
深入实施“人工智能+”行动 浪潮软件集团看好人工智能+工业质检广阔前景,持续布局线缆行业智能质检
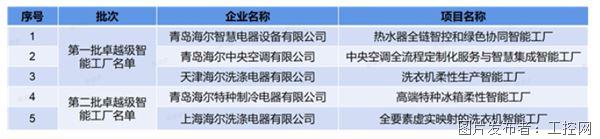
海尔新增2家卓越级智能工厂,总数品类行业双第一
深度剖析格力打破磁悬浮压缩机国外垄断,底气来自对自主创新的坚守!








 投诉建议
投诉建议