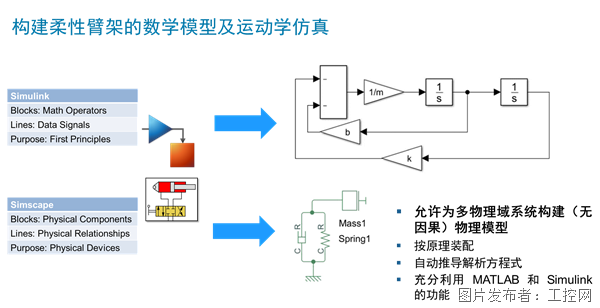
基于MATLAB的机器人电液伺服控制系统设计

   本文以复杂的机器人的电液伺服控制系统作为研究对象,对电液伺服系统的在机器人上的应用建模和仿真. 利用Labview、 Matlab／Simulink等仿真软件对电液伺服控制系统进行动态仿真，对于改进系统的设计以及提高液压系统的可靠性都具有重要意义。

前言

   电液伺服系统具有响应速度快、调速范围广、比功率大、耐用性高等优点，在车辆船舶、工程机械、武器系统等方面得到了广泛的应用。为了进行电液伺服系统的分析、仿真与控制，需要构造电液伺服系统的模型，但其固有的流量-压力曲线、液体压缩、电磁转换、饱和摩擦等非线性因素，使得难以获得电液伺服系统的精确模型。

   电液位置伺服系统主要是用于解决位置跟随的控制问题，其根本任务就是通过执行机构实现被控量对给定量的及时和准确跟踪，并要具有足够的控制精度。电液伺服系统的动态特性是衡量一套电液伺服系统设计及调试水平的重要指标。它由电信号处理装置和若干液压元件组成，元件的动态性能相互影响，相互制约及系统本身所包含的非线性，致使其动态性能复杂。因此，电液伺服控制系统的设计及仿真受到越来越多的重视。

   本文以比例方向阀实现对伺服油缸的位置控制，加入位移传感器构成位置闭环控制系统。采用NI公司的USB-6008数据采集卡完成数据采集、数据输出控制等多项功能，以LABVIEW和MATLAB混合编程实现了良好的实时控制功能。

1 液压系统特性简述

   随着液压技术的不断发展与进步和应用领域与范围的不断扩大，系统柔性化与各种性能要求更高，采用传统的以完成执行机构预定动作循环和限于系统静态性能的系统设计远远不能满足要求。因此，现代液压系统设计研究人员对系统动态特性进行研究，了解和掌握液压系统动态工作特性与参数变化，以提高系统的响应特性、控制精度以及工作可靠性，是非常必要的。

   液压系统动态特性是其在失去原来平衡状态到达新的平衡状态过程中所表现出来的特性，原因主要是由传动与控制系统的过程变化以及外界干扰引起的。在此过程中，系统各参变量随时间变化性能的好坏，决定系统动态特性的优劣。系统动态特性主要表现为稳定性（系统中压力瞬间峰值与波动情况）以及过渡过程品质（执行、控制机构的响应品质和响应速度）问题。

   液压系统动态特性的研究方法主要有传递函数分析法、模拟仿真法、实验研究法和数字仿真法等。数字仿真法是利用计算机技术研究液压系统动态特性的一种方法。先是建立液压系统动态过程的数字模型——状态方程，然后在计算机上求出系统中主要变量在动态过程的时域解。该方法适用于线性与非线性系统，可以模拟出输入函数作用下系统各参变量的变化情况，从而获得对系统动态过程直接、全面的了解，使研究人员在设计阶段就可预测液压系统动态性能，以便及时对设计结果进行验证与改进，保证系统的工作性能和可靠性，具有精确、适应性强、周期短以及费用低等优点。

2 系统原理及建模

2.1系统组成及原理

   电液位置伺服控制系统以液体作为动力传输和控制介质，利用电信号进行控制输入和反馈。只要输入某一规律的输入信号，执行元件就能启动、快速并准确地复现输入量的变化规律。控制系统结构图如图1所示：

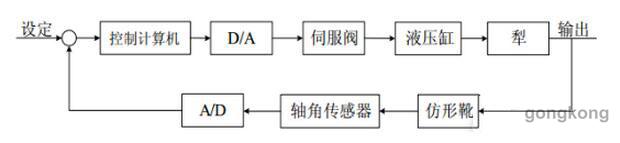              图1电液位置伺服控制系统结构图

2.2电液位置伺服系统建模

   建立电液伺服系统的传递函数，需要根据连续性方程、牛顿定律等物理法则，分别对伺服阀、液压缸等环节建立函数表达式，并联立求出系统的传递函数。具体地，需要建立伺服阀方程、伺服阀流量方程、连续性方程和力平衡方程。

2.2.1伺服阀方程

   伺服阀是具有复杂高阶非线性特性的器件。在实际中，通常可以将伺服阀简化等效为一阶系统（低频）或者二阶系统（高频）：

   其中Q为伺服阀输出流量，u为电压控制信号，Kv为伺服阀增益，τv为伺服阀时间常数。

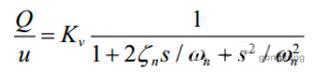
  其中ζn为伺服阀阻尼系数，ωn为伺服阀自然频率。

   上述的伺服阀带宽、增益、阻尼系数和自然频率等参数，可以查阅厂商提供的相关手册获得，从而得到伺服阀的传递函数表达式。在自动定深电液伺服系统中，伺服阀的时间常数、阻尼系数均较小，为简单起见，可以忽略伺服阀的动态特性，而直接得到伺服阀的阀芯位移与输入信号u的关系：

xv=Kvu

其中xv表示伺服阀的阀芯位移，u为电压控制信号。

2.2.2伺服阀流量方程

   为确定伺服阀的流量方程，预先假定伺服阀的控制窗口是配作且对称的，油源压力是恒定的。线性化的伺服阀流量方程为：

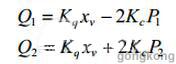
其中，Q1和Q2分别表示进油和回油流量，P1和P2分别表示进油和回油压力，Kq为阀的流量增益，Kc为阀的流量-压力系数。

由上式可得：

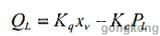
其中QL为负载流量，PL为负载压差。

2.2.3连续性方程

   为确定液压缸连续性方程，预先假设液压缸中各处压力始终是相等的，并且不会出现饱和或者空穴现象，液体流动速度很小，没有管道现象，温度和密度均为常数。对每个活塞腔应用连续性方程得：

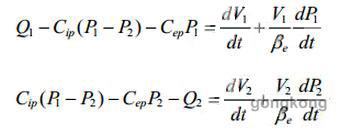
   其中V1和V2分别表示进油腔体积和回油腔体积，Cip表示活塞的内部泄露系数，Cep表示活塞的外部泄露系数，βe为系统的有效容积模数。

   通过系统给定参数和查阅伺服阀样本，计算当负载弹簧Ks=180000N/cm时，传递函数中的主要参数：放大器增益Ka=40000mA/V，ωr=0.588rad/s，ωm=200rad/s，ω0=674rad/s，ξ0=0.005。再根据系统各环节的传递函数，建立系统simulink动态模型如图2所示。

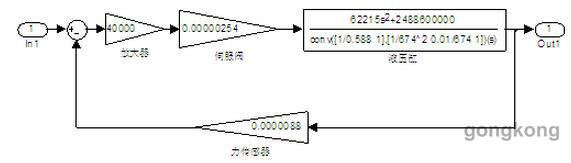
              图2系统simulink动态仿真模型

3 软件设计

   LABVIEW在线控制过程：首先进行数据采集，采集的数据是位移传感器的位移，转换为电压，送入数据采集卡的模拟量输入端AI0，程序中对模拟输入通道进行配置，主要包括配置采样通道号、最大最小值以及采样方式(差分、单端)，并输出采样波形。接着是PID算法，要设定P、I、D的参数和输出的上下限，然后是模拟量的输出，程序中对模拟量输出通道配置，输出口配置为AO0口，并配置输出的最大最小值。经过程序运算后得到的数值送给伺服放大器的输入端，驱动伺服阀，使液压缸前进或后退，完成对电液伺服系统的位置控制[3]。数据采集系统流程图如图3所示。

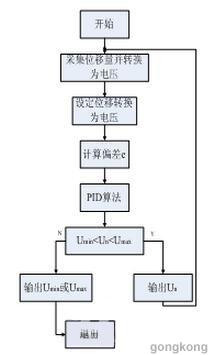
                   图3采集系统流程图

4 MATLAB仿真

   基于多层前向神经网络构造自动定深电液伺服系统的智能模型，隐含层节点数目为8，训练次数为1000次。由于神经网络参数初值的不确定会造成网络性能的不同，因此神经网络训练10次，均方根误差等性能指标取其平均值。神经网络能够较好的拟合电液伺服系统的动态特性，且模型具有较高的泛化能力仿真图如图4所示：

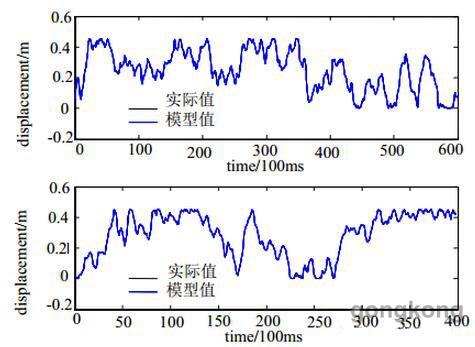
                图4电液伺服系统神经网络输出值和实际值

5 结论

    电液伺服系统是一类典型的非线性系统，本文采用机理建模和智能建模方法为进一步实现电液伺服系统的控制奠定了基础。建模过程与仿真结果表明,对系统建立正确的数学模型并进行分析仿真，分析系统的动态特性，可以有效地预见系统的输出，达到对系统工作状态的了解，提高了设计和分析系统的效率，为进一步控制系统，提高响应速度和控制精度奠定了一定的基础。